lMF系统,LMF系统概述

LMF系统概述

LMF系统，即最小均数四分法（Least Mean Fourth）系统，是一种基于数据分析的非参数方法。它通过使用均值和四分位数来优化拟合结果，以减少异常数据的影响。LMF系统在处理非高斯噪声环境和频谱很宽的白噪声时表现出色，因此在信号处理、系统识别等领域有着广泛的应用。

LMF系统的原理与特点

LMF系统的核心思想是利用均值和四分位数来估计系统的参数或特征。具体步骤如下：

收集系统的输入和输出数据。

计算数据的均值和四分位数。

基于均值和四分位数的差异，估计系统的参数或特征。

重复以上步骤，直到达到预设的拟合精度或迭代次数。

LMF系统的特点包括：

对异常数据敏感度低，能够有效减少异常数据对系统参数估计的影响。

适用于非高斯噪声环境和频谱很宽的白噪声。

计算简单，易于实现。

LMF系统在信号处理中的应用

LMF系统在信号处理领域有着广泛的应用，以下列举几个典型应用场景：

噪声消除：在信号重建过程中，对于统计特性未知或特性随时可能变化的噪声，或是频谱很宽的白噪声，LMF系统可以有效地消除噪声，提高信号质量。

信号检测：在通信系统中，LMF系统可以用于检测信号，提高检测性能。

信号调制解调：在数字通信系统中，LMF系统可以用于调制解调，提高通信质量。

LMF系统在系统识别中的应用

LMF系统在系统识别领域也有着重要的应用，以下列举几个典型应用场景：

系统参数估计：LMF系统可以用于估计系统的参数，如传递函数、频率响应等。

系统辨识：LMF系统可以用于辨识系统，如识别系统的结构、参数等。

系统优化：LMF系统可以用于优化系统，如调整系统参数，提高系统性能。

LMF系统的优势与挑战

LMF系统具有以下优势：

对异常数据敏感度低，能够有效减少异常数据对系统参数估计的影响。

适用于非高斯噪声环境和频谱很宽的白噪声。

计算简单，易于实现。

然而，LMF系统也存在一些挑战：

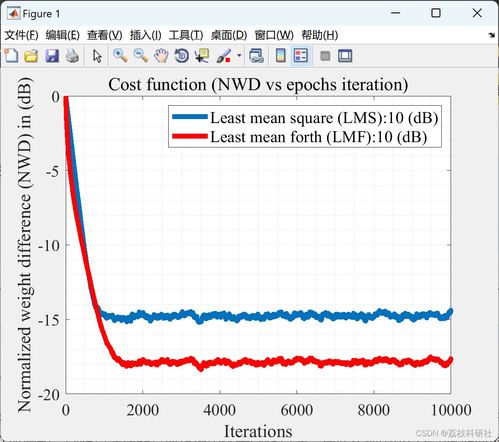
在处理高斯噪声时，LMF系统的性能可能不如最小均方（LMS）算法。

LMF系统的收敛速度较慢，可能需要较长的计算时间。

LMF系统作为一种基于数据分析的非参数方法，在信号处理和系统识别等领域具有广泛的应用。它具有对异常数据敏感度低、适用于非高斯噪声环境和频谱很宽的白噪声等优势。然而，LMF系统也存在一些挑战，如处理高斯噪声时性能不如LMS算法、收敛速度较慢等。随着技术的不断发展，LMF系统有望在更多领域发挥重要作用。