
dzy游戏
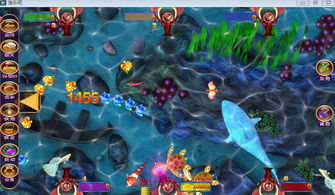
- 文件大小:
- 界面语言:简体中文
- 文件类型:
- 授权方式:5G系统之家
- 软件类型:主题下载
- 发布时间:2025-01-14
- 运行环境:5G系统之家
- 下载次数:270
- 软件等级:
- 安全检测: 360安全卫士 360杀毒 电脑管家
系统简介
哦,亲爱的读者,你是否曾在某个午后,被一阵神秘的召唤牵引,踏入了一个充满未知与冒险的世界?DZY,这位充满好奇心的游戏爱好者,就曾这样被一个古老的游戏深深吸引。让我们一起跟随他的脚步,探索这个充满陷阱与福利的迷宫,看看他能否在游戏中找到属于自己的宝藏。
迷宫初探:DZY的冒险之旅

DZY来到了一个由n个房间和m条走廊连接而成的迷宫。每个房间都可能是他前进道路上的一个转折点,而走廊则像是通往未来的桥梁。他站在迷宫的起点,第一间房间,心中充满了期待与紧张。
这个迷宫可不简单,它有着自己的规则。DZY每次都会随机选择一条走廊前进,然后回到起点,重复这个过程。而更让人紧张的是,迷宫中有些房间隐藏着陷阱,一旦踏入,就会失去一条宝贵的生命。不过,DZY也不是省油的灯,他深知只有勇敢面对,才能找到通往胜利的道路。
陷阱与福利:迷宫中的双刃剑
在这个迷宫中,陷阱和福利并存。DZY知道,如果他恰好有两条命时进入了第n号房间,那么他首先会失去一条命,但随后会开启一个福利关卡。这个关卡或许能给他带来意想不到的惊喜,或许能帮助他找到走出迷宫的线索。
陷阱的数量并不少,这无疑增加了DZY的冒险难度。他必须小心翼翼地选择每一条走廊,以免踏入陷阱。而福利关卡的出现,也让他的冒险之路充满了变数。
概率计算:开启福利关卡的机率

那么,DZY开启福利关卡的机率到底有多大呢?这需要我们进行一番计算。
首先,我们需要了解从房间u出发,到达房间v,除了房间u、v外,经过的任何房间都没有陷阱的概率,我们称之为w(u,v)。这个概率可以通过矩阵乘法来求解。
对于n个房间,我们可以构建一个n×n的矩阵,矩阵中的每个元素代表从对应房间出发,到达另一个房间的概率。我们可以通过高斯消元法来求解这个矩阵,从而得到所有w(u,v)的值。
这个过程并不简单。对于n<500的情况,时间复杂度为O(n^4),这在实际计算中是无法接受的。因此,我们需要寻找一种更高效的方法来解决这个问题。
优化算法:从O(n^4)到O(n^3)
为了提高计算效率,我们可以采用一种优化算法。首先,我们枚举起点u,设f[i]表示从起点u开始,到I且不经过陷阱点(不包括i,j)的概率是多少。
我们将黑点拆分,将问题转化为求解一系列子问题。通过这种方法,我们可以将时间复杂度从O(n^4)降低到O(n^3),从而在较短的时间内得到结果。
DZY的冒险结局:开启福利关卡的机率
经过一番计算,DZY终于得到了开启福利关卡的机率。这个概率虽然不高,但足以让他充满信心地继续冒险。他知道,只要勇敢面对,总有一天,他能够找到属于自己的宝藏。
在这个充满未知与挑战的迷宫中,DZY的冒险之旅才刚刚开始。他将继续探索,寻找那个隐藏在迷宫深处的秘密。而我们也期待着他能够成功,开启属于自己的福利关卡。
亲爱的读者,你是否也被DZY的冒险故事所吸引?在这个充满奇迹的世界里,也许你也能找到属于自己的宝藏。让我们一起期待DZY的冒险结局,期待那个属于我们的奇迹时刻。
下载地址



常见问题
- 2025-10-13 聚鲸融贷款app官方版下载
- 2025-10-13 谷歌play游戏应用最新版
- 2025-10-13 夜猫圈酒吧 [][][] 下载app
- 2025-10-13 糖糖郊游记
主题下载下载排行

其他人正在下载
- 顶级特工
- 激光和球
- 风来之国勇者传说
- 墨剑江湖最新版2024
- 阴暗的迷宫2最新版
- 过山车生活中文版
- 魔笛MAGI 摩尔迦娜XP主题+Win7主题
- 轻音少女 秋山澪XP主题+Win7主题
- 海贼王 乌索普XP主题+Win7主题
- 学园默示录 毒岛冴子XP主题+Win7主题+Win8主题



