matlab信号与系统,信号与系统基本概念
时间:2024-12-11 来源:网络 人气:
随着信息技术的飞速发展,信号与系统理论在各个领域都发挥着至关重要的作用。MATLAB作为一种功能强大的数学计算软件,在信号与系统领域有着广泛的应用。本文将介绍MATLAB在信号与系统中的应用,包括基本概念、常用函数、仿真实例等,旨在帮助读者更好地理解和应用MATLAB进行信号与系统分析。
信号与系统基本概念
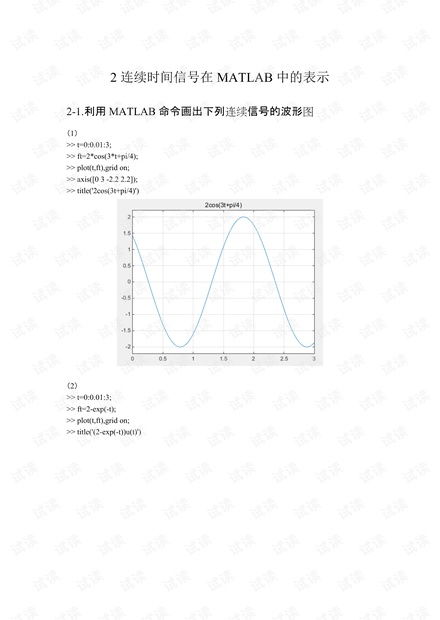
信号:表示物理量的时间函数,如声音、图像、温度等。
系统:将输入信号转换为输出信号的设备或过程。
线性时不变系统:系统对输入信号的响应只与输入信号的幅度和相位有关,与输入信号的形状无关。
非线性系统:系统对输入信号的响应与输入信号的形状有关。
MATLAB信号与系统常用函数
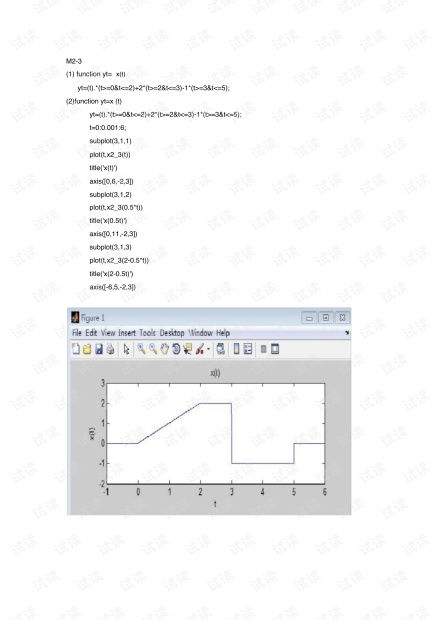
信号生成函数:如sin、cos、exp、heaviside等。
系统建模函数:如tf、zpk、ss等。
系统分析函数:如freqz、bode、step等。
信号处理函数:如fft、ifft、filter等。
信号与系统仿真实例
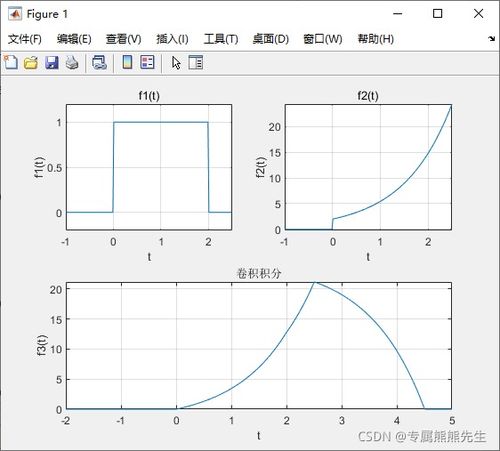
以下是一个简单的信号与系统仿真实例,演示了如何使用MATLAB进行信号生成、系统建模和系统分析。
实例1:信号生成与系统建模
假设我们要生成一个频率为10Hz的正弦信号,并将其通过一个低通滤波器进行滤波。
% 生成频率为10Hz的正弦信号
fs = 100; % 采样频率
t = 0:1/fs:1-1/fs; % 时间向量
x = sin(2pi10t); % 生成正弦信号

% 建立低通滤波器
b = [1]; % 滤波器系数
a = [1 -1]; % 滤波器系数
[y, h] = filter(b, a, x); % 滤波信号
% 绘制信号波形
subplot(2,1,1);
plot(t, x);
title('原始信号波形');
subplot(2,1,2);
plot(t, y);
title('滤波后信号波形');
实例2:系统分析
接下来,我们对上述低通滤波器进行系统分析,包括频率响应和时域响应。
% 频率响应
[h, w] = freqz(b, a, 1024, fs);
subplot(2,1,1);
plot(w, 20log10(abs(h)));
title('频率响应');
% 时域响应
[y, t] = step(b, a, t);
subplot(2,1,2);
plot(t, y);
title('时域响应');
本文介绍了MATLAB在信号与系统中的应用,包括基本概念、常用函数和仿真实例。通过本文的介绍,读者可以更好地理解和应用MATLAB进行信号与系统分析。在实际应用中,MATLAB还可以与其他工具箱结合,如通信系统工具箱、控制系统工具箱等,以实现更复杂的信号与系统分析。
相关推荐
教程资讯
教程资讯排行
- 1 hikvision门禁系统密码,Hikvision门禁系统密码设置与修改指南
- 2 macbook air a1370 系统
- 3 烟草网上订货平台,便捷购物新体验
- 4 g50换win7系统,联想G50笔记本更换Windows 7系统的详细教程
- 5 加盟订票软件,加盟订票软件,开启您的创业之旅
- 6 系统集成项目管理工程师考试考点突破,案例分析,实战练习一本通
- 7 松下伺服电机调试软件,男女老壮皆相与赋敛致奠醊以千数翻译
- 8 oa办公自动化系统设计方案,提升企业办公效率与协作能力
- 9 如何使用u盘重装win7系统,如何使用U盘重装Windows 7系统
- 10 太阳线直销系统怎么样,什么是太阳线直销系统?