lti系统稳定,什么是LTI系统？

什么是LTI系统？

线性时不变（Linear Time-Invariant, LTI）系统是信号与系统理论中的一个重要概念。它指的是那些在输入信号变化时，其输出信号也按照相同规律变化的系统。LTI系统具有线性、时不变和因果性三个基本特性。

LTI系统的线性特性

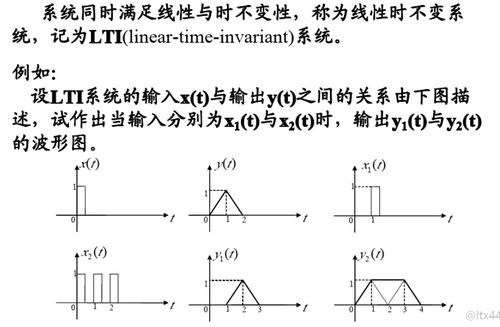
线性特性是指系统对输入信号的响应满足叠加原理。也就是说，如果系统对两个输入信号 ( u_1(t) ) 和 ( u_2(t) ) 的响应分别是 ( y_1(t) ) 和 ( y_2(t) )，那么系统对输入信号 ( u_1(t) + u_2(t) ) 的响应 ( y(t) ) 将等于 ( y_1(t) + y_2(t) )。用数学公式表示就是：( y(t) = LTI(u_1(t) + u_2(t)) = LTI(u_1(t)) + LTI(u_2(t)) )。

LTI系统的时不变特性

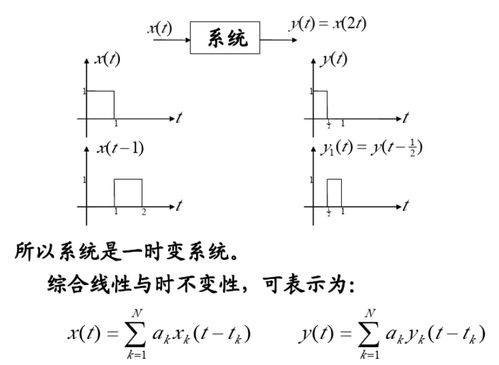
时不变特性意味着系统的特性不随时间变化。也就是说，如果将输入信号 ( u(t) ) 的时间尺度进行缩放，比如 ( u(t) rightarrow u(at) )，那么输出信号 ( y(t) ) 也会相应地缩放，即 ( y(t) rightarrow y(at) )。这可以表示为：( LTI(u(at)) = aLTI(u(t)) )，其中 ( a ) 是缩放因子。

LTI系统的因果性

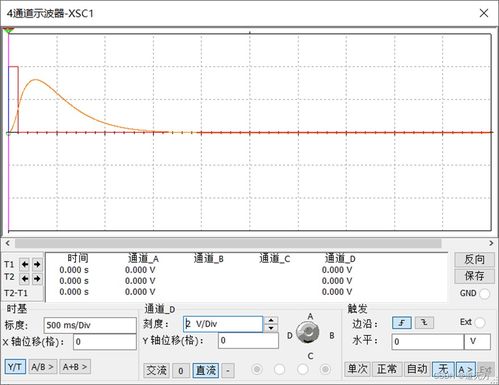
因果性是指系统的输出不会在输入之前出现。也就是说，对于任何时刻 ( t )，系统的输出 ( y(t) ) 只依赖于 ( t ) 时刻或之前时刻的输入 ( u(t) )，而与 ( t ) 时刻之后的输入无关。用数学语言描述就是：如果 ( u(t) ) 在 ( t 稳定性是LTI系统的一个重要特性，它描述了系统在受到有界输入时，输出是否也会保持有界。具体来说，一个LTI系统是BIBO（有界输入有界输出）稳定的，如果对于任何有界输入信号 ( u(t) )，其输出 ( y(t) ) 也是有界的。用数学公式表示就是：如果 ( int_{-infty}^{infty} |u(t)| dt 判断LTI系统的稳定性通常需要分析系统的传递函数或差分方程。对于传递函数，可以通过检查其极点是否全部位于复平面的左半平面来判断系统的稳定性。对于差分方程，可以通过求解其特征方程的根来判断系统的稳定性。

LTI系统是信号与系统理论中的基础概念，它在通信、控制、滤波等领域有着广泛的应用。理解LTI系统的线性、时不变和因果性特性，以及如何判断系统的稳定性，对于从事相关领域的研究和工程实践具有重要意义。