matlab动力学系统仿真,理论与实践结合的完美典范

Matlab动力学系统仿真：理论与实践结合的完美典范

随着科学技术的不断发展，动力学系统仿真在工程、物理、生物等多个领域发挥着越来越重要的作用。Matlab作为一种功能强大的科学计算软件，在动力学系统仿真中具有广泛的应用。本文将详细介绍Matlab动力学系统仿真的基本原理、方法以及在实际应用中的案例。

一、Matlab动力学系统仿真的基本原理

Matlab动力学系统仿真主要基于以下原理：

数学建模：通过对动力学系统进行数学建模，将实际问题转化为数学模型。

数值求解：利用数值方法求解数学模型，得到动力学系统的动态响应。

可视化：将仿真结果以图形、曲线等形式展示，便于分析和理解。

二、Matlab动力学系统仿真的方法

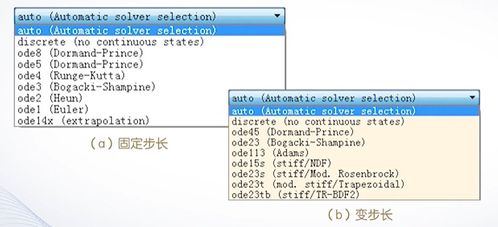
Matlab动力学系统仿真主要采用以下方法：

常微分方程（ODE）求解：适用于线性或非线性常微分方程的求解。

状态空间模型：将动力学系统表示为状态空间形式，便于进行控制设计。

传递函数：将动力学系统表示为传递函数形式，便于进行频域分析。

三、Matlab动力学系统仿真实例

以下是一个简单的Matlab动力学系统仿真实例，用于模拟一个单摆的运动。

1. 建立数学模型

单摆的运动方程为：$ddot{theta} + frac{g}{l} sin theta = 0$，其中$theta$为摆角，$g$为重力加速度，$l$为摆长。

2. 编写Matlab代码

```matlab

function pendulum_simulation()

% 定义参数

g = 9.81; % 重力加速度

l = 1; % 摆长

theta0 = pi/4; % 初始摆角

omega0 = 0; % 初始角速度

tspan = [0 10]; % 仿真时间范围

% 定义微分方程

odefun = @(t, y) [y(2); -g/lsin(y(1))];

% 求解微分方程

[t, y] = ode45(odefun, tspan, [theta0 omega0]);

% 绘制仿真结果

plot(t, y(:,1));

xlabel('Time (s)');

ylabel('Angle (rad)');

title('Single Pendulum Motion');

3. 运行仿真

在Matlab命令窗口中运行`pendulum_simulation`函数，即可得到单摆的运动曲线。

四、Matlab动力学系统仿真的优势

Matlab动力学系统仿真具有以下优势：

易于实现：Matlab提供了丰富的数学函数和工具箱，方便用户进行动力学系统仿真。

可视化：Matlab强大的图形功能，可以将仿真结果以直观的方式展示出来。

可扩展性：Matlab支持模块化编程，便于用户扩展和改进仿真模型。

Matlab动力学系统仿真是一种高效、实用的方法，在各个领域都得到了广泛应用。通过本文的介绍，相信读者对Matlab动力学系统仿真有了更深入的了解。在实际应用中，用户可以根据具体问题选择合适的仿真方法，充分发挥Matlab的优势，为科学研究和技术创新提供有力支持。