matlab离散系统的阶跃响应,离散系统的阶跃响应

在数字信号处理和控制系统中，离散系统的阶跃响应是一个重要的分析工具。它可以帮助我们了解系统在受到阶跃输入时的动态行为，从而评估系统的性能。本文将介绍如何使用MATLAB来求解和绘制离散系统的阶跃响应，并探讨相关的性能指标。

离散系统的阶跃响应

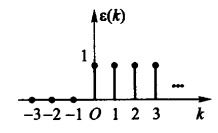
离散系统的阶跃响应是指系统在单位阶跃输入下的输出响应。单位阶跃输入可以表示为：[ u(k) = begin{cases}

1, & text{if } k geq 0

0, & text{if } k 在MATLAB中，我们可以使用`stepz`函数来求解和绘制离散系统的阶跃响应。以下是一个简单的例子：

```matlab

% 定义系统的系数

b = [1 2 3];

a = [1 -1.5 0.5];

% 使用stepz函数绘制阶跃响应

stepz(b, a);

title('离散系统的阶跃响应');

xlabel('时间 (k)');

ylabel('输出');

在上面的代码中，`b`和`a`分别代表系统的分子和分母系数。`stepz`函数会自动计算系统的阶跃响应，并绘制出响应曲线。

性能指标分析

阶跃响应的性能指标包括上升时间、调整时间、峰值时间和超调量等。以下是对这些性能指标的解释：

上升时间：从阶跃响应开始到达到稳态值的90%所需的时间。

调整时间：从阶跃响应开始到达到并保持在稳态值的2%以内所需的时间。

峰值时间：阶跃响应达到峰值所需的时间。

超调量：阶跃响应峰值与稳态值之差与稳态值的比值。

在MATLAB中，我们可以使用`stepinfo`函数来获取阶跃响应的性能指标。以下是一个例子：

```matlab

% 获取阶跃响应的性能指标

[h, t] = stepz(b, a);

stepinfo(h, t);

% 打印性能指标

fprintf('上升时间: %f 秒

', stepinfo.RiseTime);

fprintf('调整时间: %f 秒

', stepinfo.SettlingTime);

fprintf('峰值时间: %f 秒

', stepinfo.PeakTime);

fprintf('超调量: %f%%

', stepinfo.Overshoot);

本文介绍了如何使用MATLAB求解和绘制离散系统的阶跃响应，并探讨了相关的性能指标。通过分析阶跃响应，我们可以更好地了解系统的动态行为，从而为系统设计和优化提供依据。