matlab 系统频率响应,连续系统频率响应分析

在电子工程、通信工程和自动控制等领域，系统频率响应的分析是至关重要的。MATLAB作为一种强大的数学计算和仿真软件，提供了丰富的工具和函数来帮助工程师和分析人员研究系统的频率响应特性。本文将详细介绍如何在MATLAB中计算和分析系统的频率响应，包括连续系统和离散系统的频率响应分析。

连续系统频率响应分析

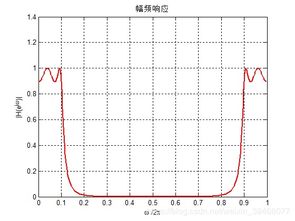
连续系统的频率响应可以通过Bode图和Nyquist图来分析。Bode图展示了系统增益和相位随频率的变化，而Nyquist图则提供了系统稳定性的直观表示。

使用Bode图分析连续系统频率响应

在MATLAB中，可以使用`bode`函数来绘制系统的Bode图。以下是一个简单的例子：

num = [1 0]; % 系统的分子多项式系数

den = [1 2 3]; % 系统的分母多项式系数

bode(num, den);

这段代码将绘制一个二阶系统的Bode图。`num`和`den`分别代表系统传递函数的分子和分母多项式系数。

使用Nyquist图分析连续系统频率响应

Nyquist图可以通过`nyquist`函数在MATLAB中绘制。以下是一个绘制Nyquist图的例子：

num = [1 0]; % 系统的分子多项式系数

den = [1 2 3]; % 系统的分母多项式系数

nyquist(num, den);

这个函数将绘制出系统在复平面上的Nyquist轨迹，从而可以分析系统的稳定性。

离散系统频率响应分析

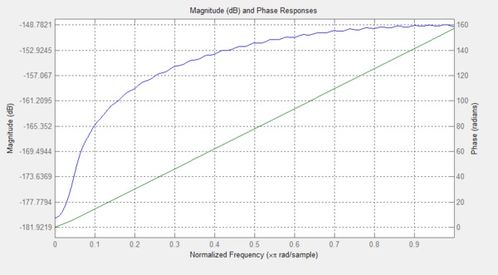
离散系统的频率响应分析通常涉及离散时间傅里叶变换（DTFT）和离散傅里叶变换（DFT）。在MATLAB中，可以使用`freqz`函数来计算离散系统的频率响应。

使用freqz函数分析离散系统频率响应

以下是一个使用`freqz`函数计算离散系统频率响应的例子：

num = [1 0]; % 系统的分子多项式系数

den = [1 2 3]; % 系统的分母多项式系数

npoints = 1024; % 频率点的数量

freqz(num, den, npoints);

这段代码将计算并绘制离散系统的频率响应。`npoints`参数指定了频率点的数量，这将影响频率响应曲线的分辨率。

系统稳定性分析

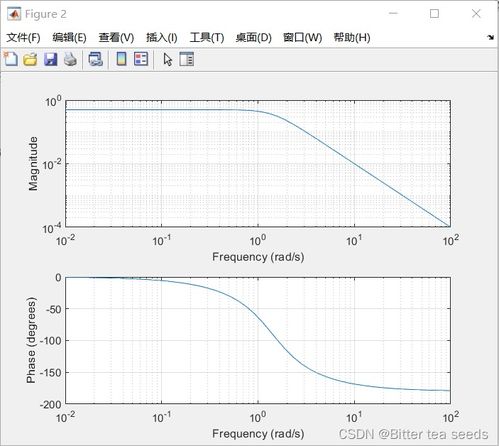
系统稳定性是工程设计和分析中的一个关键因素。在MATLAB中，可以使用`isstable`函数来检查系统是否稳定。

使用isstable函数检查系统稳定性

以下是一个检查系统稳定性的例子：

num = [1 0]; % 系统的分子多项式系数

den = [1 2 3]; % 系统的分母多项式系数

isstable(num, den);

如果系统是稳定的，`isstable`函数将返回`true`，否则返回`false`。

结论

MATLAB提供了强大的工具来分析和计算系统的频率响应。通过使用Bode图、Nyquist图、freqz函数和isstable函数，工程师和分析人员可以深入理解系统的频率特性，从而进行有效的系统设计和优化。